
개발자를 위한 실전 선형대수학(Practical Linear Algebra for Data Science)
5장 행렬, 파트 2 : 행렬의 확장 개념
행렬 노름
- 벡터 노름: 유클리드 기하학적 길이로 벡터 원소의 제곱합의 제곱근으로 계산됨.
Q. 행렬의 노름은 어떤 개념인가?
A. 행렬을 특정짓는 하나의 숫자라는 점에서 벡터 노름과 유사하다. 하지만 단 하나의 행렬 노름은 없어, 여러 개의 서로 다른 노름을 가진다.
각 행렬 노름은 서로 다른 의미를 가진다. 수많은 행렬 노름은 크게 원소별 계열과 유도 계열로 구분된다.
유클리드 노름/프로베니우스 노름(Frobenius Norm)
- 원소별 계열의 노름으로, 모든 행렬 원소의 제곱합의 제곱근으로 계산됨
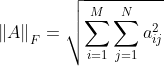
프로베니우스 노름은 l2 노름이라고 한다.
(l2 노름은 원소별 p-노름에 대한 일반공식에서 이름을 딴 것, p=2일 때가 프로베니우스 노름)

행렬 노름은 머신러닝과 통계 분석의 여러 곳에서 응용되고 있음. 그중에서 정규화(regularization)은 중요한 응용임
정규화 → 모델 적합성을 개선, 일반화 성능을 높임
정규화 기본적인 아이디어는 최소화 알고리즘에 비용함수로 행렬노름을 대입하는 것이다.
노름은 모델 매개변수가 너무 커지거나(l2 정규화, 릿지 회귀), 희소 결과가 나오는 것을 방지한다(l1 정규화, 라쏘 회귀).
프로베니우스 노름은 행렬 거리를 계산할 때도 응용됨
- 동일한 행렬 사이의 거리는 0, 행렬의 원소의 차이가 클수록 거리가 증가
- 이미지 데이터의 크기 축소 등에서 활용(원본 데이터 행렬과 거리가 최소인 축소 데이터 행렬을 계산)
행렬의 대각합과 프로베니우스 노름
- 행렬의 대각합(trace)은 대각 원소의 합이며 tr(A)로 나타냄(정방 행렬에 대해서만 존재)
행렬의 대각합은 행렬의 고윳값의 합과 같고, 결국 행렬의 고유공간(eigenspace)의 '부피'에 대한 측정치가 된다.
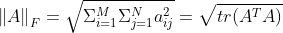
- 즉 프로베니우스 노름은 어떤 행렬의 전치와 그 행렬을 곱한 결과의 대각합의 제곱근으로 계산할 수 있음
이것이 성립하는 이유는 행렬 A^T A의 각 대각 원소는 동일한 행에 대한 내적이기 때문이다.
행렬공간
"행렬 공간은 전통 및 응용 선형대수학의 많은 주제에서 핵심적인 개념입니다. 다행스럽게도 행렬 공간의 개념은 어렵지 않습니다. 근본적으로 행렬의 서로 다른 특징들 사이의 선형 가중 결합입니다."
https://youtu.be/bvB5uQXX7WY?si=4MMNNxyKACxHJScW
연립 방정식을 행렬의 형태로 나타낸다
= 행렬은 선형변환에 대응한다. 즉 변환 후 v가 되는 벡터 x를 찾는 것과 같다. (연립 선형방정식의 기하적 해석)
변환 A가 공간을 하위 차원으로 찌끄러뜨리 않는 이상(det(a) = 0 이지 않는 이상,
변환이 이루어지기 전으로 돌리는 변환을 할 수 있다.( 역행렬이 존재한다)
랭크 : 변환 이후 출력된 차원의 수
열공간
벡터에서 선형 가중 결합은 벡터 집합에 스칼라를 곱하고 합하는 것
▶ 하나의 특정 스칼라 집합으로 연산하는 대신 무한 개의 스칼라로 벡터 집합을 무한히 결합할 수 있다.
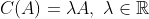
C(A)는 행렬 A의 열공간을 나타낸다.
행공간
전치된 행렬의 열 공간
영공간
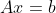
A의 열의 가중 결합으로 벡터 b를 생성하는 어떤 가중치 집합 x를 찾는다
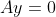
A의 열의 가중 결합이 영벡터가 되는 어떤 가중치 집합 y를 찾는다
-> 임의의 행렬 A에 대해 성립하는 정답(y=0)이 존재함
→ 그렇다면 모든 값이 0이 아닌 가중치 집합이 존재하는가?
계수(rank) 하나의 행렬과 연관된 고유한 숫자이다.
계수의 속성들
- 계수는 음이 아닌 정수값을 가진다
- 모든 행렬이 고유한 계수를 가진다
- 행렬의 계수는 r(A), rank(A)로 나타낸다, A는 계수-r 행렬이라 읽는다.
- 행렬의 최대로 가능한 계수는 행 또는 열의 개수 중에서 더 작은 값
- 최대 계수를 가지는 행렬를 최대 계수(Full rank)라고 한다
- 0이 아닌 스칼라 곱셈은 행렬 계수에 영향을 미치지 않는다
행렬 계수에 대한 동일한 해석과 정의
- 선형 독립 집합을 형성하는 최대 열(또는 행)의 수
- 열공간의 차원의 수(행공간의 차원의 수와 동일)
- 행렬 안의 정보를 포함하는 차원의 수(선형 종속적일 가능성이 있으므로 행렬의 전체 열 또는 행 수와 같지 않음)
- 행렬에서 0이 아닌 특잇값의 수
"행렬의 열공간과 행공간이 다르지만 행렬 공간의 차원의 수는 동일하다. 그리고 그 차원의 수는 행렬의 계수이다."
'Datascience > Linear Algebra' 카테고리의 다른 글
| [개발자를 위한 선형대수학] 행렬의 확장 개념(2) (0) | 2024.01.24 |
|---|---|
| 1장 연습문제 (1) | 2024.01.22 |
| [개발자를 위한 실전 선형대수학] 행렬과 행렬의 기본 연산 (1) | 2024.01.21 |
| [개발자를 위한 실전 선형대수학] 벡터의 응용 (0) | 2024.01.21 |
| [개발자를 위한 실전 선형대수학] 벡터의 확장 개념 (0) | 2024.01.14 |

개발자를 위한 실전 선형대수학(Practical Linear Algebra for Data Science)
5장 행렬, 파트 2 : 행렬의 확장 개념
행렬 노름
- 벡터 노름: 유클리드 기하학적 길이로 벡터 원소의 제곱합의 제곱근으로 계산됨.
Q. 행렬의 노름은 어떤 개념인가?
A. 행렬을 특정짓는 하나의 숫자라는 점에서 벡터 노름과 유사하다. 하지만 단 하나의 행렬 노름은 없어, 여러 개의 서로 다른 노름을 가진다.
각 행렬 노름은 서로 다른 의미를 가진다. 수많은 행렬 노름은 크게 원소별 계열과 유도 계열로 구분된다.
유클리드 노름/프로베니우스 노름(Frobenius Norm)
- 원소별 계열의 노름으로, 모든 행렬 원소의 제곱합의 제곱근으로 계산됨
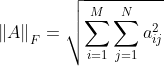
프로베니우스 노름은 l2 노름이라고 한다.
(l2 노름은 원소별 p-노름에 대한 일반공식에서 이름을 딴 것, p=2일 때가 프로베니우스 노름)

행렬 노름은 머신러닝과 통계 분석의 여러 곳에서 응용되고 있음. 그중에서 정규화(regularization)은 중요한 응용임
정규화 → 모델 적합성을 개선, 일반화 성능을 높임
정규화 기본적인 아이디어는 최소화 알고리즘에 비용함수로 행렬노름을 대입하는 것이다.
노름은 모델 매개변수가 너무 커지거나(l2 정규화, 릿지 회귀), 희소 결과가 나오는 것을 방지한다(l1 정규화, 라쏘 회귀).
프로베니우스 노름은 행렬 거리를 계산할 때도 응용됨
- 동일한 행렬 사이의 거리는 0, 행렬의 원소의 차이가 클수록 거리가 증가
- 이미지 데이터의 크기 축소 등에서 활용(원본 데이터 행렬과 거리가 최소인 축소 데이터 행렬을 계산)
행렬의 대각합과 프로베니우스 노름
- 행렬의 대각합(trace)은 대각 원소의 합이며 tr(A)로 나타냄(정방 행렬에 대해서만 존재)
행렬의 대각합은 행렬의 고윳값의 합과 같고, 결국 행렬의 고유공간(eigenspace)의 '부피'에 대한 측정치가 된다.
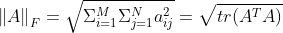
- 즉 프로베니우스 노름은 어떤 행렬의 전치와 그 행렬을 곱한 결과의 대각합의 제곱근으로 계산할 수 있음
이것이 성립하는 이유는 행렬 A^T A의 각 대각 원소는 동일한 행에 대한 내적이기 때문이다.
행렬공간
"행렬 공간은 전통 및 응용 선형대수학의 많은 주제에서 핵심적인 개념입니다. 다행스럽게도 행렬 공간의 개념은 어렵지 않습니다. 근본적으로 행렬의 서로 다른 특징들 사이의 선형 가중 결합입니다."
https://youtu.be/bvB5uQXX7WY?si=4MMNNxyKACxHJScW
연립 방정식을 행렬의 형태로 나타낸다
= 행렬은 선형변환에 대응한다. 즉 변환 후 v가 되는 벡터 x를 찾는 것과 같다. (연립 선형방정식의 기하적 해석)
변환 A가 공간을 하위 차원으로 찌끄러뜨리 않는 이상(det(a) = 0 이지 않는 이상,
변환이 이루어지기 전으로 돌리는 변환을 할 수 있다.( 역행렬이 존재한다)
랭크 : 변환 이후 출력된 차원의 수
열공간
벡터에서 선형 가중 결합은 벡터 집합에 스칼라를 곱하고 합하는 것
▶ 하나의 특정 스칼라 집합으로 연산하는 대신 무한 개의 스칼라로 벡터 집합을 무한히 결합할 수 있다.
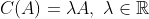
C(A)는 행렬 A의 열공간을 나타낸다.
행공간
전치된 행렬의 열 공간
영공간
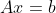
A의 열의 가중 결합으로 벡터 b를 생성하는 어떤 가중치 집합 x를 찾는다
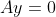
A의 열의 가중 결합이 영벡터가 되는 어떤 가중치 집합 y를 찾는다
-> 임의의 행렬 A에 대해 성립하는 정답(y=0)이 존재함
→ 그렇다면 모든 값이 0이 아닌 가중치 집합이 존재하는가?
계수(rank) 하나의 행렬과 연관된 고유한 숫자이다.
계수의 속성들
- 계수는 음이 아닌 정수값을 가진다
- 모든 행렬이 고유한 계수를 가진다
- 행렬의 계수는 r(A), rank(A)로 나타낸다, A는 계수-r 행렬이라 읽는다.
- 행렬의 최대로 가능한 계수는 행 또는 열의 개수 중에서 더 작은 값
- 최대 계수를 가지는 행렬를 최대 계수(Full rank)라고 한다
- 0이 아닌 스칼라 곱셈은 행렬 계수에 영향을 미치지 않는다
행렬 계수에 대한 동일한 해석과 정의
- 선형 독립 집합을 형성하는 최대 열(또는 행)의 수
- 열공간의 차원의 수(행공간의 차원의 수와 동일)
- 행렬 안의 정보를 포함하는 차원의 수(선형 종속적일 가능성이 있으므로 행렬의 전체 열 또는 행 수와 같지 않음)
- 행렬에서 0이 아닌 특잇값의 수
"행렬의 열공간과 행공간이 다르지만 행렬 공간의 차원의 수는 동일하다. 그리고 그 차원의 수는 행렬의 계수이다."
'Datascience > Linear Algebra' 카테고리의 다른 글
| [개발자를 위한 선형대수학] 행렬의 확장 개념(2) (0) | 2024.01.24 |
|---|---|
| 1장 연습문제 (1) | 2024.01.22 |
| [개발자를 위한 실전 선형대수학] 행렬과 행렬의 기본 연산 (1) | 2024.01.21 |
| [개발자를 위한 실전 선형대수학] 벡터의 응용 (0) | 2024.01.21 |
| [개발자를 위한 실전 선형대수학] 벡터의 확장 개념 (0) | 2024.01.14 |
