
개발자를 위한 실전 선형대수학(Practical Linear Algebra for Data Science)
5장 행렬, 파트 2 : 행렬의 확장 개념
계수의 응용
벡터가 열공간에 존재하나요?
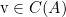
벡터가 행렬의 열공간에 있는지 여부는 선형대수학에서 중요한 부분이다.
→ "행렬 계수를 이해해야 확장 가능한 방식으로 이 부분에 대한 답을 찾을 수 있다."
행렬의 확장(augmenting) (첨가행렬)
- 행렬의 우측에 열을 추가한다
https://en.wikipedia.org/wiki/Augmented_matrix
Augmented matrix - Wikipedia
From Wikipedia, the free encyclopedia Matrix formed by appending columns of two other matrices In linear algebra, an augmented matrix ( A | B ) {\displaystyle (A\vert B)} is a k × ( n + 1 ) {\displaystyle k\times (n+1)} matrix obtained by appending a k {\
en.wikipedia.org
벡터가 행렬의 열공간에 있는지 여부를 확인하는 알고리즘은 다음과 같음
- 벡터로 행렬을 확장합니다.(원래 행렬 A, 확장된 행렬 ~A)
- 두 행렬의 계수를 계산합니다
- 두 계수를 비교합니다. 두 가지 가능한 결과가 있습니다.
계수 비교 결과 ▼
1) rank(A) = rank(~A) 벡터는 행렬 A의 열공간에 있습니다.
2) rank(A) < rank(~A) 벡터는 행렬 A의 열공간에 없습니다.
알고리즘의 근거
- 벡터가 행렬의 열공간에 있다면, 벡터가 A의 열들의 선형 가중 결합으로 나타낼 수 있다.
= 확장 행렬 ~A의 열들은 선형 종속 집합이 된다.
- 생성 측면에서 벡터 v는 ~A에서 중복이다. 따라서 계수는 그대로 유지된다.
- 반대로 벡터가 행렬의 열공간에 없다면, 벡터를 A의 열들의 선형 가중 결합으로 나타낼 수 없다.
= 확장 행렬 ~A의 열들은 선형 독립 집합이다.
이는 벡터 v가 ~A에 새로운 정보를 추가했다는 뜻이다. 그리고 계수가 1만큼 증가한다는 것을 의미한다.
이는 분산 분석, 회귀, 일반 선형 모델의 기초가 되는 선형 최소제곱 모델링의 추론 일부이기 때문이다.
여기서 우리가 알아야 할 기본 개념은 세상이 어떻게 돌아가는지에 대한 모델을 개발하고 그 모델을 행렬로 변환한다는 것입니다.(설계행렬, Design Matrix)
실제 세계에서 측정한 데이터를 벡터로 저장한다. 만약 데이터 벡터가 설계 행렬의 열공간에 존재한다면 우리는 세상을 완벽하게 모델링한 것이다. 실제로는 거의 모든 데이터 벡터가 열공간에 없기 때문에 통계적으로 유의미한 것으로 간주될 수 있을 만큼 열공간의 데이터와 충분히 가까운지 확인합니다.
벡터 집합의 선형 독립성
벡터 집합의 선형 독립성을 검증하는 알고리즘
▶ 벡터를 행렬에 넣고, 행렬의 계수를 계산한 다음 해당 행렬의 최대로 가능한 계수와 비교함
행렬식(determinant)
- 행렬식은 정방 행렬과 관련된 숫자
-
'Datascience > Linear Algebra' 카테고리의 다른 글
| [개발자를 위한 실전 선형대수학] 역행렬 (0) | 2024.01.27 |
|---|---|
| [개발자를 위한 실전 선형대수학] 행렬 응용: 데이터 분석에서의 행렬 (0) | 2024.01.25 |
| 1장 연습문제 (1) | 2024.01.22 |
| [개발자를 위한 실전 선형대수학] 행렬의 확장 개념(1) (1) | 2024.01.21 |
| [개발자를 위한 실전 선형대수학] 행렬과 행렬의 기본 연산 (1) | 2024.01.21 |
