[개발자를 위한 실전 선형대수학] 벡터의 응용

 

개발자를 위한 실전 선형대수학(Practical Linear Algebra for Data Science)

3장 벡터 응용: 데이터 분석에서의 벡터

 

 

 

 

---

벡터와 벡터 연산이 데이터 과학에서 어떻게 사용되는가?

 

상관관계와 코사인 유사도

 

상관관계

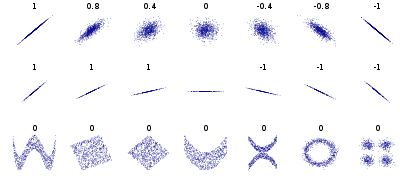
상관관계는 통계와 머신러닝에서 가장 근본적이면서 중요한 분석 방법

상관계수(correlation coefficient): 두 변수 사이의 선형관계를 정량화한 하나의 숫자

 → 정규화가 포함됨(단위의 영향 x, 상관계수가 기대하는 -1 ~ +1의 범위를 가지게 됨)

 

 

https://ko.wikipedia.org/wiki/%ED%94%BC%EC%96%B4%EC%8A%A8_%EC%83%81%EA%B4%80_%EA%B3%84%EC%88%98

 

-> 상관계수 계산에 포함된 두 정규화

1. 각 변수의 평균 중심화: 평균중심화는 각 데이터 값에서 평균값을 빼는 것

2. 벡터 노름 곱으로 내적을 나누기: 측정 단위를 제거하고 상관계수의 최대 크기를 1로 조정하는 정규화

 

피어슨 상관계수 수학적 공식

선형대수학 용어로 나타낸 피어슨 상관계수

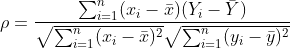
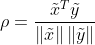
~x는 x를 평균 중심화한 값,

 

피어슨 상관계수(Pearson Correlation Coefficient)은 변수의 크기로 정규화된 두 변수 사이의 내적

 

코사인 유사도(Cosine similarity)

코사인 유사도는 두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도를 의미

두 벡터의 방향이 완전히 동일한 경우에는 1의 값을 가지며, 90°의 각을 이루면 0, 180°로 반대의 방향을 가지면 -1의 값을 갖는다. 즉, 결국 코사인 유사도는 -1 이상 1 이하의 값을 가지며 값이 1에 가까울수록 유사도가 높다고 판단할 수 있음.

 

코사인 유사도

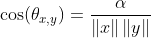
(알파는 두 변수의 내적)

코사인 유사도 = 평균 중심화가 포함되지 않은 피어슨 상관계수

 

피어슨 상관계수와 코사인 유사도가 두 변수 사이의 선형관계를 반영할 수 있는 이유

▶ 벡터의 선형연산인 내적을 기반으로 하기 때문

 

 

k- 평균 클러스터링(k-means clustering)

그룹 중심까지의 거리를 최소화하도록 다변랑 데이터를 상대적으로 적은 수(k)의 그룹 또는 범주로 분류하는 비지도 기법

 

- k- 평균 클러스터링 알고리즘

1. 데이터 공간에서 임의의 k개 중심점을 초기화
2. 각 데이터 관측치와 각 중심 사이의 유클리드 거리를 계산
3. 각 데이터 관측치를 가장 가까운 중심의 그룹에 할당함
4. 그룹의 평균치를 계산하여, 중심을 새롭게 갱신
5. 수렴 기준을 만족할 때까지, 위 과정을 반복